🍐Κ3 - Τελεστές
Πριν προχωρήσουμε στην εκχώρηση μεταβλητών πρώτα θα μάθουμε για τους τελεστές και τις εκφράσεις. Επίσης θα μάθουμε για την ιεραρχία εκτέλεσης των τελεστών σε μία έκφραση.
Τελεστές είναι τα σύμβολα τα οποία δηλώνουν την πράξη η οποία θα εκτελεστεί ανάμεσα σε δύο τελεστέους. Οι τελεστέοι μπορούν να είναι μεταβλητές, σταθερές, αριθμοί ή συναρτήσεις.
π.χ.
15 + a
Οι εκφράσεις είναι συνδυασμός μεταβλητών, τελεστών, αριθμών και παρενθέσεων σε μία παράσταση.
π.χ.
15 + 2*3 / 20 - (-9 - 13)
ΙΕΡΑΡΧΙΑ ΤΕΛΕΣΤΩΝ
Η ισχύς των τελεστών δεν είναι ίδιες. Άλλοι είναι πιο ισχυροί, άλλοι πιο αδύναμοι και άλλοι ισοδύναμοι. Αυτό συμβαίνει ώστε να γίνεται μια προτεραιοποίηση και να μην δημιουργείται πρόβλημα ή σύγχυση κατά της εκτέλεσή τους στις εκφράσεις.
π.χ.
15 + 2*3 / 20 - (-9 - 13)
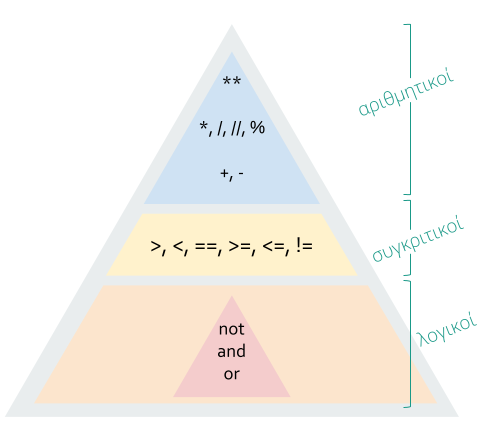
🔷 σε περίπτωση ίδιας δυναμικότητας τότε πρώτο γίνεται αριστερά → δεξιά
📌 Όσο πιο υψηλή η θέση ενός τελεστή στην Ιεραρχία («Πυραμίδα») τόσο πιο σύντομα εκτελείται έναντι των άλλων τελεστών που έχουν χαμηλότερη θέση.
Ας δούμε κάποια παραδείγματα Αριθμητικών τελεστών:
4 ** 3 ⇒ 4 * 4 * 4 ⇒ 64
2 * 3 ⇒ 6
15 / 2 ⇒ 7.5
9 - 19 ⇒ -10
13 // 2 ⇒ 6
13 % 2 ⇒ 1
Επίσης, κάποια παραδείγματα Συγκριτικών τελεστών:
5 > 6 ⇒ False
15 == 8+7 ⇒ True
-1 >= -14 ⇒ True
8 != 10 ⇒ True
Ας δούμε και κάποια παραδείγματα με Λογικούς τελεστές:
not 5 > 6 ⇒ True
Αυτό συμβαίνει γιατί πρώτα εκτελείται ο συγκριτικός τελεστής > επειδή έχει μεγαλύτερη θέση στην ιεραρχία των τελεστών και μετά στο αποτέλεσμα της πράξης αυτής εφαρμόζεται ο τελεστής not ο οποίος μετατρέπει το False → True.
Ας δούμε και ένα πιο πολύπλοκο παράδειγμα με Λογικούς τελεστές, αλλά πρώτα θα χρειαστεί να μάθουμε για τον Πίνακα Αλήθειας (Truth Table).
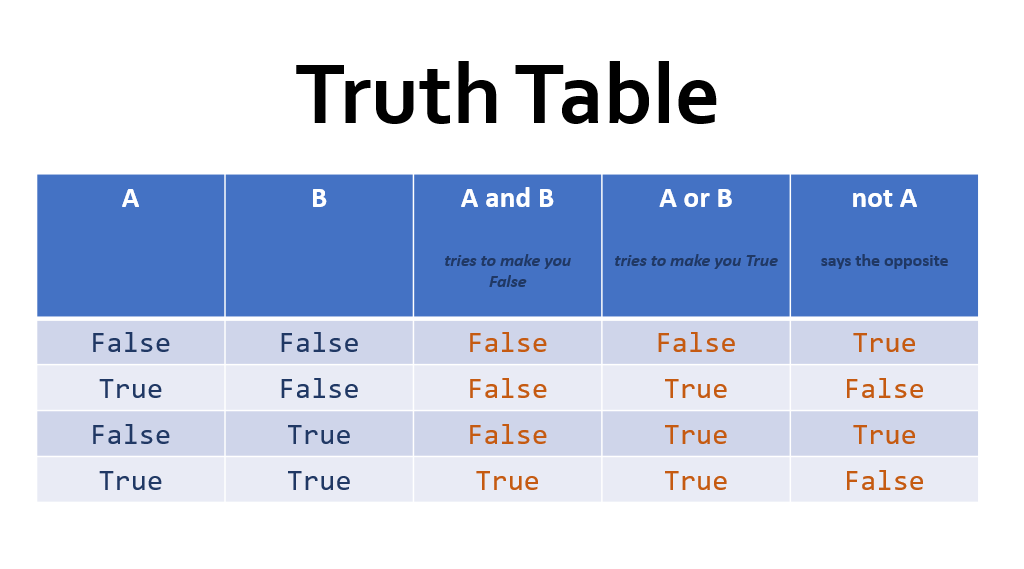
Φανταστείτε ότι ένας έφηβος (Α) και η μικρή του αδερφή (Β) θέλουν να πάνε να δουν Καραγκιόζη στην πλατεία του χωριού τους. Έτσι λοιπόν, ρωτούν την μητέρα τους ώστε να τους δώσει την άδεια.
Ωραία, τώρα που είδαμε τον Πίνακα Αλήθειας ας επιστρέψουμε στο 2ο παράδειγμα των Λογικών τελεστών.
-10 > -100 or (19 + 2 > 25 and 25 ** 2 > 125) ⇒
True or (False and True) ⇒
True or True ⇒
True
Παράδειγμα 01 - Εκφράσεις με Τελεστές
Οι τιμές θα είναι το αποτέλεσμα των εκφράσεων ύστερα από την εφαρμογή της Ιεραρχίας Τελεστών.
π.χ.
a = 4**2 + 9
a = 25 # ← αποτέλεσμα της a μεταβλητής
b = not 5 == 5
b = False # ← αποτέλεσμα της b μεταβλητής
Παράδειγμα 02 - Εκφράσεις με Τελεστές v2
⚙️Άσκηση 01 - Εκφράσεις με Τελεστές
| α) | 10 % 3 |
| β) | 24 // 23 |
| γ) | 1+2**3 |
| δ) | 10 % 6 |
| ε) | 19 / 2 |
⚙️Άσκηση 02 - Εκφράσεις με Τελεστές
| α) | 10 == 9+2 and -1 > -12 |
| β) | 59 // 58 == 1 |
| γ) | not True and False |
| δ) | 12-24 < -1 |
| ε) | not ( -1 < -100 ) |
⚙️Άσκηση 03 - Εκφράσεις με Τελεστές
| α) | 8**2/2 |
| β) | 17 // 2 |
| γ) | -1 > -10 and 3 == 7 - 4 |
| δ) | not 3**3 == 27 |
| ε) | 64/8*3 |
⚙️Άσκηση 04 - Εκφράσεις με Τελεστές
| α) | 37 // 5 |
| β) | not (2**3 == 3**2) and (4 == 6-2) |
| γ) | 25 == 5**5 |
| δ) | 2**3 > 3**2 and 14 == 7*2 |
| ε) | not (2**3 == 3**2) and (4 == 6-2) |
⚙️Τεστ 1 - Εκφράσεις με Τελεστές
⚙️Τεστ 2 - Εκφράσεις με Τελεστές